[1주 BCI 기초 다지기] 7일차: CSP 알고리즘, Common Spatial Pattern

7일차: Common Spatial Pattern (CSP) 알고리즘 (25-01-30)

1. EEG 분석에서 CSP를 사용하는 이유

CSP란?

https://what-i-want-to-do.tistory.com/66

해당 게시물에서 이미 설명한 바와 같이, EEG와 같은 데이터를 두 개 이상의 클래스로 분류하기 위해 공간적 특징을 추출하는 알고리즘이다.

주로 BCI에서는 좌/우 손 움직임 분류와 같은 작업에 사용된다.

CSP를 사용하는 이유

1. 뇌파 데이터의 공간적 분포 활용

    EEG 신호는 전극의 공간적 분포에 따라 변하는데, CSP는 이를 최적화해 특정 클래스 간 차이를 극대화.

2. 특정 주파수 대역에서의 차이 강조

    좌/우 손 움직임 같은 작업에서는 특정 주차수 대역에서 신호가 다르게 나타나며, CSP는 이를 효율적으로 추출.

3. 특징 차원의 축소

    고차원 EEG 데이터를 저차원 공간으로 변환함으로써 계산 비용을 줄이고 분류 성능을 향상.

4. 이진 분류에서의 강점

    CSP는 특히 이진 클래스를 구별하는데 뛰어난 성능을 보임.

2. MATLAB에서의 실습

오늘의 실습에서는 임의의 예제 데이터를 생성하여 진행해 볼 것이다.

데이터 생성하기

clear all; close all; clc;

%class 1 data
n = 500;
x1(:,1) = randn(n, 1);
x1(:,2) = x1(:,1) + randn(n, 1);
figure;
plot(x1(:,1), x1(:,2), 'b*')

%class 2 data
x2(:,1) = randn(n, 1);
x2(:,2) = 3*x2(:,1) + randn(n, 1); %기울기 변화
hold on;
plot(x2(:,1), x2(:,2), 'ro')

서로 다른 특성을 지닌 두 class의 데이터를 생성했다. 이제 이 데이터들이 서로 잘 구분되도록 CSP를 적용해 보자.

하나의 데이터에 대해서는 분산이 최대, 다른 하나의 데이터에 대해서는 분산이 최소가 되는 벡터를 찾은 다음에 원래의 데이터에 곱해주면 분류가 잘 되는 데이터가 된다. 이것이 CSP의 원리이다.

 

%CSP
[csp, csp_d] = eig(cov(x1), cov(x2)); %'x' 데이터는 반드시 [trial * features] 형태

csp_v = [[0;0], csp(:,2)];
csp_v1 = [[0;0], csp(:,1)];

%데이터에 CSP 적용하기
csp_x1 = x1 * csp;
csp_x2 = x2 * csp;
figure;
plot(csp_x1(:,1), csp_x1(:,2), 'b*', csp_x2(:,1), csp_x2(:,2), 'ro');
hold on;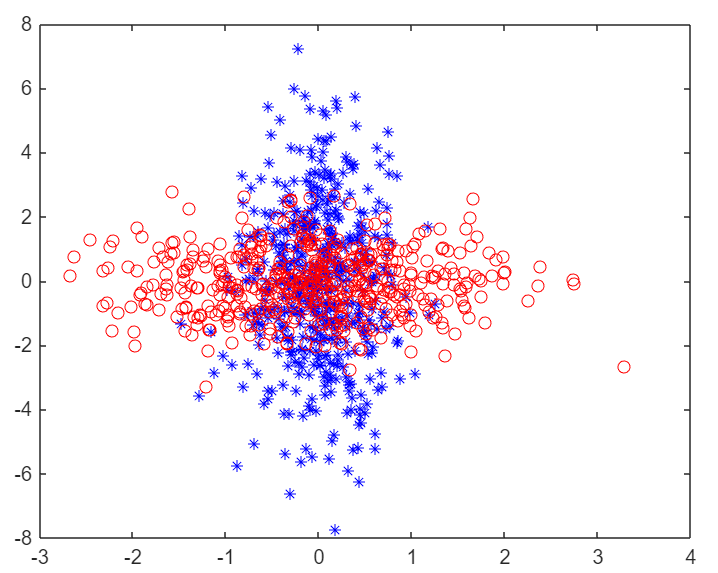

두 class의 데이터가 잘 분리된 것을 확인할 수 있다.