Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 분산표현
- 의료윤리
- neurotalk
- BCI
- AI
- 신경과학
- csp 알고리즘
- matlab
- 미겔
- 잠재변수
- latent variable
- speech reconstruction
- 헬싱키 선언
- HPC
- 책
- imagined speech
- brain-to-speech
- 표현학습
- Distributed Representation
- 뇌과학
- csp알고리즘
- neural representation learning
- 기준음성
- 뇌와 세계
- common spatial pattern
- AI윤리
- 블록체인
- spoken speech
- gt voice
- 발화의도
Archives
- Today
- Total
o0y0o
[1주 BCI 기초 다지기] 4일차: 아티팩트 제거, EOG, EMG, ICA, fastICA 본문
4일차: EEG 신호의 전처리 II (25-01-25)
1. 아티팩트 제거 개념
아티팩트란?
- 정의
- 아티팩트(artifact)는 EEG 신호에 포함된 비뇌파 신호로, 분석에 방해가 되는 잡음이기에 부가적인 제거가 필요함.
- 아티팩트의 종류
- Eye Blink (EOG)
- 눈 깜박임으로 인한 신호.
- 보통 전두엽(Frontal, Fp1, Fp2)에 영향을 미쳐 큰 진폭으로 나타남.
- 근전도 (EMG)
- 근육 움직임에 의한 신호.
- 주로 30 Hz 이상에서 강하게 나타남.
- 전력선 노이즈
- 주변 전기 기기나 전력선에서 발생하는 일정한 주파수의 신호.
- 50 Hz(또는 60 Hz)에서 발셍힘.
- 전극 접촉 불량
- 전극이 두피에 제대로 접촉하지 않아 발생하는 느리고 큰 폭의 신호.
- Eye Blink (EOG)
아티팩트 제거 방법
- 필터링
- 전력선 노이즈와 같은 특정 주파수 제거.
- 3일차에서 다룬 Band-pass 및 Notch 필터로 처리 가능.
- 수동 제거
- 눈에 띄는 큰 아티팩트가 있는 구간 혹은 trial을 제거하거나 마스크 처리.
- Independent Component Analysis (ICA)
- EEG 신호를 독립적인 신호 성분으로 분리해 아티팩트를 제거.
- 오늘 다룰 주요 기법!
2. ICA(Independent Component Analysis)
ICA(독립성분분석, Independent Component Analysis)란?
- 정의
- 다변량의 신호를 통계적으로 독립적인 하부 성분으로 분리하는 계산 방법.
- 즉, 관찰된 다채널 EEG 데이터를 독립적인 뇌파 성분과 아티팩트 성분으로 분리하는 데 자주 사용됨.
- 원리
- 관찰된 신호 X는 여러 독립적인 신호 S가 혼합된 결과로 표현할 수 있음.
X=A⋅S
X∈R^(n×T): 관찰된 신호 (n개의 채널, T개의 샘플).
S∈R^(m×T): 독립적인 신호 성분 (m≤n).
A∈R^(n×m): 혼합 행렬 (unknown).
이때 ICA의 목표는 A와 S를 추정하여 X를 분리하는 것. - 뇌파 신호 X의 S에서 아티팩트를 제거하고 나머지 신호를 다시 조합하는 기법이 ICA 기반 아티팩트 제거.
- ICA는 다음 세 가지 주요 가정을 기반으로 작동함.
- 독립성 (Independence): S의 각 성분 S1,S2,…,Sm은 통계적으로 독립적이어야 함.
- 비가우시안성 (Non-Gaussianity): S의 분포는 가우시안 분포가 아니어야 함. (가우시안 분포에서는 독립 성분을 추정할 수 없음)
- 혼합 행렬 A의 정칙성: A는 정칙 행렬로 가정, (열백터가 선형독립이어야 함.)
- 이하 Whitening, 독립 성분 분리, 독립 성분 정렬 및 출력의 단계로 신호를 재구성할 수 있음.
- 관찰된 신호 X는 여러 독립적인 신호 S가 혼합된 결과로 표현할 수 있음.
3. MATLAB에서의 실습
사전 설정
- fastICA 라이브러리 설치
- MATLAB Add-On에서 ICA를 검색해 “PCA and ICA Pakage” 설치.
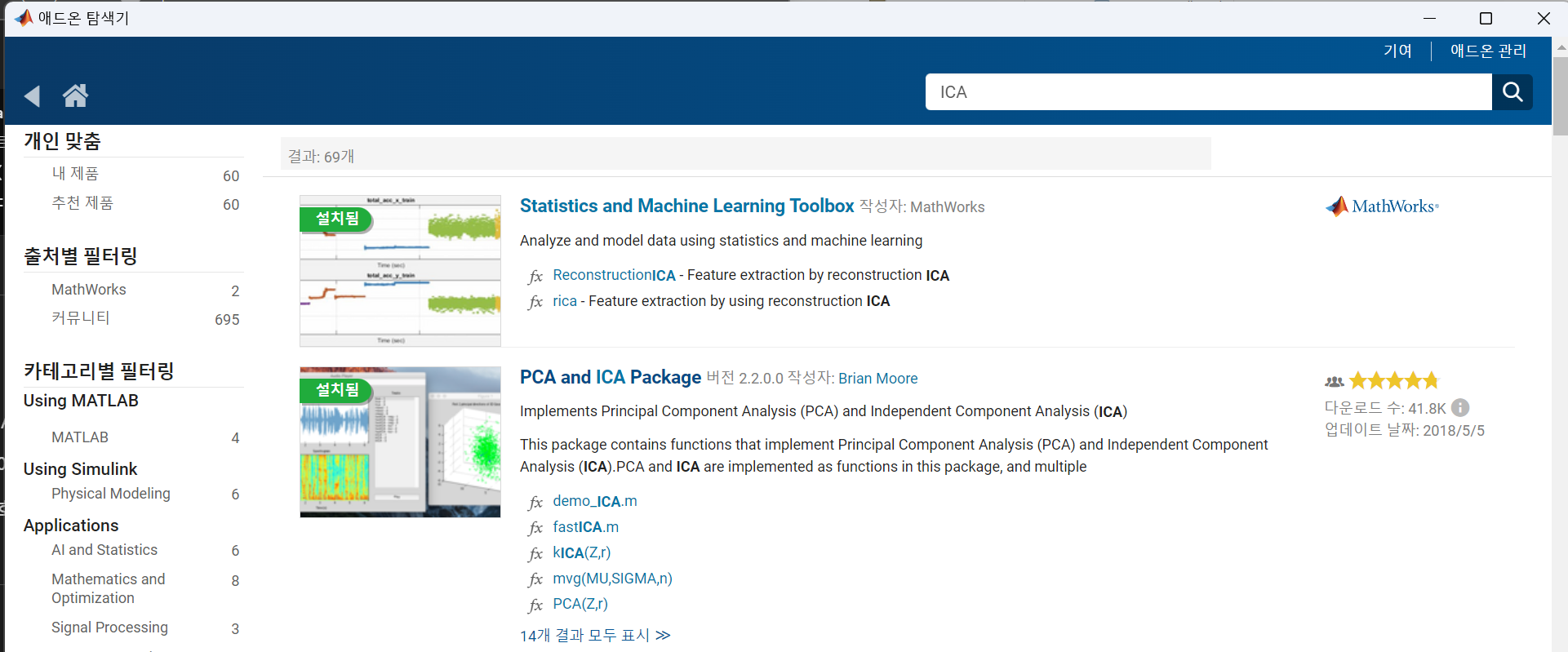
본 글에선 두 번째 목록의 PCA and ICA Pakage을 사용함.
- MATLAB Add-On에서 ICA를 검색해 “PCA and ICA Pakage” 설치.
- 다채널 예제 데이터 생성
- ICA는 다변량(EEG 신호에서는 다채널) 데이터에서 사용 가능한 기법이므로, 3일차에서 사용한 rawData를 다채널로 확장.
% 다채널 데이터 생성 rawData_multi = [rawData; rawData + 1 * sin(2 * pi * 1 * t);]; % 다채널 데이터 시각화 for i = 1:2 subplot(2, 1, i); plot(t, rawData_multi(i, :)); title([num2str(i), '번째 데이터']); xlabel('Time (s)'); ylabel('Amplitude'); end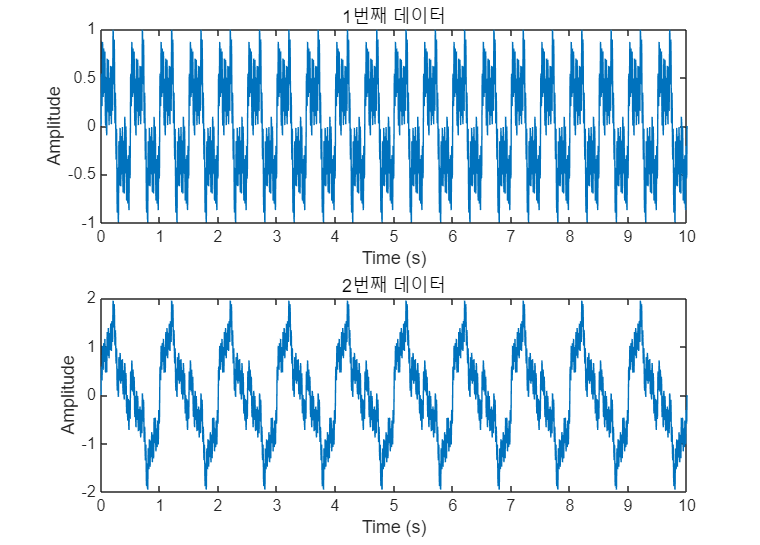
- 위의 코드로 생성한 데이터에 ICA 분석을 적용하면 sin(2 * pi * 1 * t) 성분이 분리될 것을 기대할 수 있음.
- ICA는 다변량(EEG 신호에서는 다채널) 데이터에서 사용 가능한 기법이므로, 3일차에서 사용한 rawData를 다채널로 확장.
예제 데이터와 fastICA를 이용한 실습
- ICA 수행
% fastICA 적용 [ICs, mixingMatrix, separatingMatrix] = fastICA(rawData_multi, 2); % [독립성분, 분리행렬, 화이트닝행렬, 데이터평균] % 2: 추출할 독립 성분의 개수. % 독립 성분 시각화 figure; for i = 1:2 subplot(2, 1, i); plot(t, ICs(i, :)); title(['Independent Component ', num2str(i)]); xlabel('Time (s)'); ylabel('Amplitude'); end
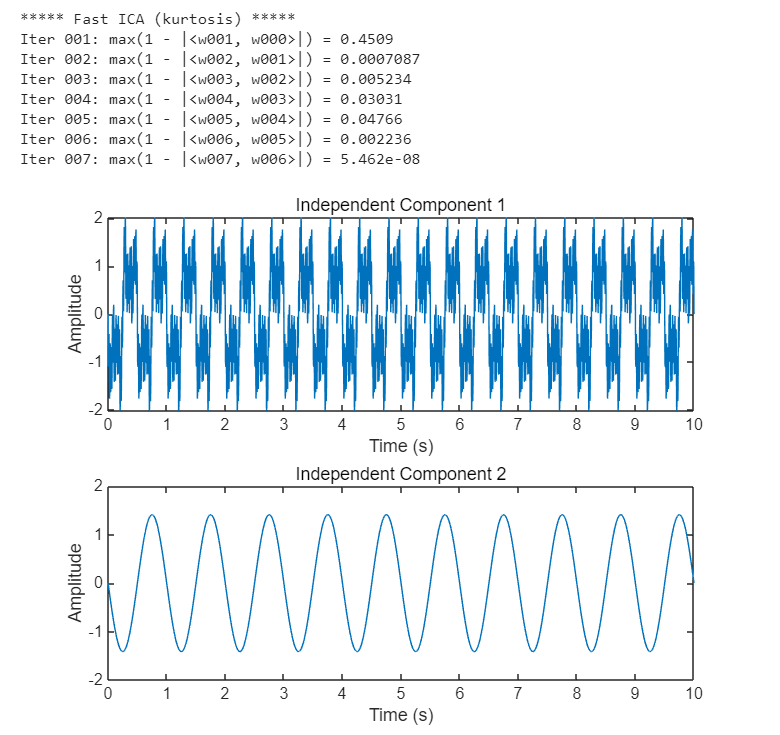
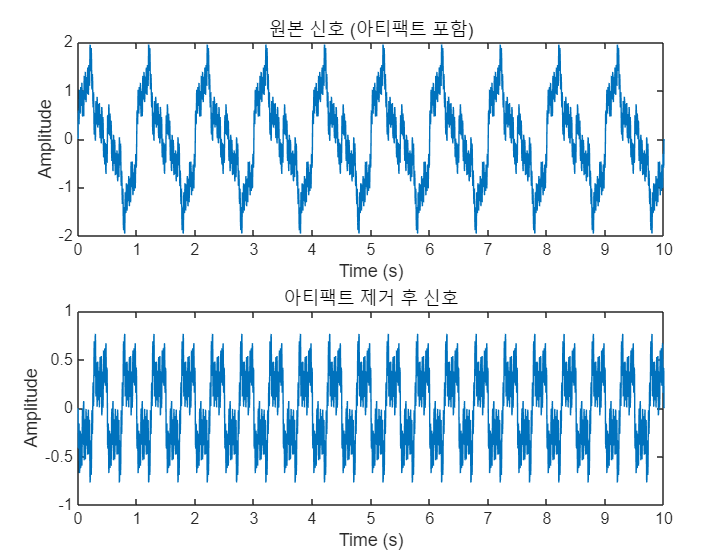
- 아티팩트 제거 및 신호 재구성
% 다채널 데이터 생성 rawData_multi = [rawData; rawData + sin(2 * pi * 1 * t);]; % 다채널 데이터 시각화 for i = 1:2 subplot(2, 1, i); plot(rawData_multi(i, :)); title([num2str(i), '번째 데이터']); xlabel('Time (s)'); ylabel('Amplitude'); end
'BCI > 1주 BCI 기초 다지기' 카테고리의 다른 글
| [1주 BCI 기초 다지기] 6일차: 파워 스펙트럼 분석, PSD (0) | 2025.01.28 |
|---|---|
| [1주 BCI 기초 다지기] 5일차: 시간 영역 분석, 주파수 영역 분석, FFT (0) | 2025.01.27 |
| [1주 BCI 기초 다지기] 3일차: IIR, FIR, Band-pass, Notch 필터 (0) | 2025.01.25 |
| [1주 BCI 기초 다지기] 1-2일차: BCI 정의, EEG, 10-20 system, 뇌파 주파수 대역, 전극, 프로그램 (1) | 2025.01.24 |
| [1주 BCI 기초 다지기] 1주 학습 계획 (0) | 2025.01.24 |




